0. Info
- Section date: 9/13
- Associated lectures: 9/5, 9/7
- Associated pset: Pset 1, due 9/15
- Where to find me
- Section: Wednesdays 3-4:15pm, see section info on Canvas for location.
- Section will always cover content for the pset due on Friday (in two days)
- Specifically, this means we’ll focus on the lectures from the previous week (six and eight days previous), and not the lecture from the day before section
- Office Hours: Wednesdays 7-9pm, see office hours info on Canvas/Google Calendar for location. I will often stay for the office hours that come right after (Wednesday 9-11pm), and occasionally may drop by at the Thursday 7:30-9:30pm office hours in the same location as well.
- Section: Wednesdays 3-4:15pm, see section info on Canvas for location.
- Syllabus clarifications
- Problem Sets: due Fridays at 5pm. They will cover content up to the previous week (e.g., up to the lecture 8 days before the due date).
- Attendance: If your grade ends up being slightly below a grade cutoff, attendance in lecture in section may boost you over. Attendance (or lack thereof) will not be used to penalize.
- Me: Srihari Ganesh (senior)
- Concentrating in Chemical & Physical Biology and Math w/ a master’s in Stat
- Doing computational biology research in diffusion models for protein structure generation
- Love teaching Stat + playing IM sports on the side
- Happy to chat about everything though I’m not an expert on anything
1. Set Theory
A set is an unordered collection of unique items. For example, $A = \{ 8, 1, 2 \}$ is a set with items (elements) $8$, $1$, and $2$.
- Sets are unordered, so $\{8, 1, 2 \} = \{2, 8, 1\}$.
- Sets contain unique elemnts, so $\{8, 1, 2, 1\}$ is NOT a set.
- Sets are a collection of any type of item, so $\{A, B, C\}$, $\{\text{car, cow, walnut}\}$, and $\{$❤️, 👨🏫, ⏳$\}$ are all sets.
1.1 Definitions
$A$ is a subset of $B$ (notated $A \subset B$ or $A \subseteq B$) if every element of $A$ is also an element of $B$.
The empty set (notated $\emptyset$) is the set with no elements, $\{\}$.
The union (notated $A \cup B$) is the set of all elements that are in $A$ or $B$ (or both).
The intersection (notated $A \cap B$) is the set of all elements that are in both $A$ and $B$.
$A$ and $B$ are disjoint if $A$ and $B$ share no elements (notated $A \cap B = \emptyset$)
- A collection of sets $A_1, \ldots, A_n$ are disjoint if no pair of sets shares any elements ($A_i \cap A_j = \emptyset$ for all $i, j$)
A collection of sets $B_1, B_2, \ldots, B_n$ are a partition of $B$ if
- $B_1, B_2, \ldots, B_n$ are disjoint, and
- $B_1 \cup B_2 \cup \cdots \cup B_n = B$.
Intuitively, $B_1, B_2, \ldots, B_n$ are (non-overlapping) puzzle pieces that form the the puzzle, $B$, when put together.
The complement of a set $A$ (notated $A^c$) is the set of all elements not in $A$
- Complements have to be taken relative to some superset $S$ (notated $A \subset S$). We think of this set as the “universe” that $A$ lives in, and is usually implied by context.
- ex. Let $S = \{1, 2, 3 \}, A = \{1, 3\}$. Then $A^c = \{2\}$.
- Note that $A$ and $A^c$ partition $S$.
The difference between two sets $B \setminus A$ is the set of all elements in $B$ which are not in $A$.
- Note that $B \cap A$, $B \setminus A$ partition $B$.
- An equivalent notation is $B \setminus A = B \cap A^c$.
The cardinality of a set, |A|, indicates the size of the set. For finite sets, it is the number of elements in the set.
We notate set membership in the following way: letting $A = \{8, 1, 2\}$,
- “$2$ is in $A$” is notated $2 \in A$.
- “$0$ is not in $A$” is notated $0 \notin A$.
1.2 Verbal Understanding
We want to think about basic set operations in words.
- $x \in A$ reads as “$x$ is in $A$”.
- We tend to work with sets by thinking about whether some variable or number is in the (e.g., whether or not $x \in A$) instead of just looking at the set written out like $A = \{8, 1, 2\}$.
- $A \cup B$ reads as “$A$ or $B$”. So we can say $x \in A \cup B$ intuitively reads as “$x$ is in $A$ or $x$ is in $B$”.
- Be careful to note that we are using the inclusive or, so $A \textit{ or } B$ means $A$, $B$, or both.
- $A \cap B$ reads as “$A$ and $B$”. So $x \in A \cap B$ reads as “$x$ is in $A$ and $x$ is in $B$”.
- $A^c$ reads as “not $A$”, so $x \in A^c$ reads as “$x$ is not in $A$”
We can apply this so see that the two versions of the set difference are equivalent. $x \in B \setminus A$ reads as “$x$ is in $B$ but not in $A$”, while $x \in B \cap A^c$ reads as “$x$ is in B and in $A^c$ (i.e., not in $A$).”
What if we have multiple operations in the same expression?
- $x \in (A \cap B)^c$ reads as “$x$ is not in both $A$ and $B$”. This means that either $x$ is not in $A$ or $x$ is not in $B$, so $x \in A^c \cup B^c$.
- $x \in (A \cup B)^c$ read as “$x$ is not in $A$ or $B$”. This means that $x$ is not in $A$ and $x$ is not in $B$, so $x \in A^c \cap B^c$. We see in the next section that these statements are essentially DeMorgan’s laws.
1.3 DeMorgan’s Laws
By talking through the expressions, you should eventually be able to convince yourself that the laws are true.
These videos also walk through the process visually:
2. Counting
2.0 Some useful problem-solving strategies (lifted from 9/5 lecture)
- Try simple/extreme cases (i.e., set $n$ to be a small number and brute-force)
- For each tool below, we’ll motivate it with an example. You can click the drop-down to view the example.
- Give objects of interest names or ID numbers
- Draw a diagram
- Make a story
2.1 Multiplication Rule
How many different combinations can you make? If an ice cream parlor has $4$ different flavors and $3$ different cup sizes, there are $4 \times 3 = 12$ different orders I could make. This example exhibits all of the above problem-solving strategies. We took the general multiplication rule (see general statement below) and, made a story about an ice cream parlor, and set $a = 4$, $b=3$. We drew a diagram (the tree below), and gave the objects (flavors and cup sizes) names in that diagram.Click for example
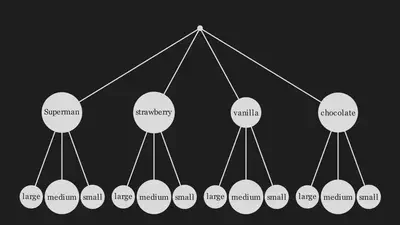
General statement: Say the outcome of a full experiment is given by the outcomes of two-subexperiments, $A$ and $B$. If sub-experiment $A$ has $a$ possible outcomes and sub-experiment $B$ has $b$ possible outcomes, then the full experiment has $a \times b$ possible outcomes.
- Note here that this will work as long as the outcome of $A$ doesn’t change the number of possible outcomes of $B$, even if $A$ changes which outcomes are possible for $B$.
2.2 Factorial
How many ways can you order $n$ distinct items? How many ways can $n=52$ card deck of cards be shuffled? I have $52$ options for the first card, then $52-1 = 51$ options for the second card, $52-2 = 50$ options for the third card, and so on. The total number of ways is thus $$52 \times 51 \times 50 \times \cdots \times 2 \times 1.$$Click for example
General statement: We use the factorial, $n!$, as a shorthand for this specific application of the multiplication rule. We have $n$ choices for the first item; we can then pick $(n-1)$ choices for the second item, and so on, giving $$ n! = n \times (n-1) \times (n-2) \cdots \times 2 \times 1. $$
2.3 Permutations
How many ways can you choose an ordered collection of $k$ distinct items from a set of $n$ distinct items? I want to take a $k=3$ week trip in New England, spending each week in a different state. New England has $n=6$ states, so using the multiplication rule, I have $6 \times 5 \times 4 = 120$ possible trips I can go on.Click for example
Be careful with off-by-one errors when you’re listing consecutive integers.
For a list of $k$ consecutive integers, the first and last numbers should have a difference of $k-1$.
For example, the list “$3, 4, 5, 6$” has $4$ items, so the difference between the first and last numbers if $6-3 = 3 = 4-1$.
How many ways can you order a set of $n$ items, where some items are repeated? How many anagrams (orderings/permutations) are there of the word “BANANA”? In other words, how many $n=6$ letter words have 3 A’s, 1 B, and 2 N’s? If we treated the letters as distinct, there would be $6!$ ways to order them. However, the 3 A’s are identical, so we are overcounting. For example, if we artificially distinguish the A’s, we see thatClick for example
“BANANA”, “BANANA”, “BANANA”, “BANANA”, “BANANA”, and “BANANA”
are all counted as different words. This means there we are overcounting the orderings of the 3 A’s by $3!$, so we can divide to get $6!/3!$.
Similarly, we are overcounting the orderings of the 2 N’s by $2!$. There is only one B, so we are not overcounting that. This gives a final answer of $\frac{6!}{3!2!} = 120$ orderings.
General statement: say we have $n$ items total with $m$ types, made up of $n_1$ items of type 1, $n_2$ items of type 2, and so forth, with $n = \sum_{i=1}^m n_i$. Then the number of permutations is \begin{equation} \frac{n!}{n_1! n_2! \cdots n_m!}. \end{equation}
2.4 Binomial Coefficient
How many ways can you choose an unordered group of $k$ items, without replacement, from a set of $n$ distinct items?
In order words, if a set has $n$ elements, how many subsets with exactly $k$ elements does it have?
Click for example
From my $n=4$ nuclear family members, how many ways can I choose $k=2$ of them to go on an all-expenses paid trip to Cambridge, Massachusetts with me?
I can use the multiplication rule, so I have $4$ options for the first family member and $3$ options for the second. However, I don’t care about the order, so I can divide by $2!$ to get $\frac{4 \times 3}{2!} = 6$ unordered groups of $2$ family members.
General statement: Using our previous permutation result, we can first pick $k$ items in order: $n \times (n-1) \times \cdots \times (n-k+1) = \frac{n!}{(n-k)!}$.
Since we don’t care about the order, we can then correct our overcounting by dividing by $k!$ to get the answer, which is called the binomial coefficient: \begin{equation} \binom{n}{k} = \frac{n!}{k!(n-k)!}. \end{equation}
2.5 Counting Subsets
How many ways can you select an unordered group of items (of any size, including $0$), without replacement, from a set of $n$ distinct items?
Alternatively worded, given a set of size $n$, how many different subsets can you come up with (including the empty set)?
The first item of the set is either in the the group or not, so there are 2 possibilities. This applies for each item in the set — it is either in the group or not. We can apply the multiplication rule to get the that the number of possible groups is \begin{equation} 2 \times 2 \times \cdots \times 2 = 2^n. \end{equation}
2.6 Bose-Einstein
How many ways can you choose an unordered group of $k$ items, with replacement, from a set of $n$ items?
Click for example
At a donut shop with $n=3$ different flavors, how many ways distinct orders of $k=5$ donuts can I make?
Let’s start with smaller values of $n$ and up the complexity. With only $n=1$ flavor, there’s only one possible order (all donuts of one flavor). With $n=2$ flavors (e.g., frosted and glazed), the order is uniquely determined by how many frosted donuts there are; for example, if we have $3$ frosted donuts, we know there must be $5-3$ glazed donuts. In the example below, we say that the donuts to the left of the divider are frosted, and those to the right are glazed.
For larger $n$, we follow a similar idea and count in a clever way. Your order can be uniquely represented by how many donuts of each flavor you buy, so we can think of placing dividers between donuts to uniquely represent our order. Each “box” created by the dividers represents a flavor: those to the left of the first divider are frosted, between the first and second divider are glazed, between the second and third divider are jam, etc.
Note that we need $4-1 = 3$ dividers to create $4$ categories. So how do we count ways to put $2$ dividers among $5$ donuts? We’ll count by treating dividers as distinguishable, then correct for the overcounting later. We have $5+1=6$ options for where to put the first divider (to the left of the first donut, between the first and second donut, etc.). The second divider has $5+1+1=7$ optinos, since there are now $6$ items ($5$ donuts, $1$ divider) that we can go between or to the left/right of. The third divider has $5+2+1=8$ options. By this pattern, we have $6 \times 7 \times 8$ ways to place dividers. However, the dividers themselves don’t tell us anything about how the donuts are divied up - only their locations - so we don’t care about the order they were placed. Thus, we divide by $3!$ ways to order the dividers to get $\frac{6 \times 7 \times 8}{3!} = \binom{8}{3}$.
Another way to think about this is that we have $5 + (4-1) = 8$ “slots” (donuts and dividers) in a row, and we need to pick out the locations of the $3$ dividers. We can use the binomial coefficient to do this in $\binom{8}{3}$ ways.
I encourage you to check out the example above for much of the derivation of the Bose-Einstein counting method.
General statement: We are trying to split the $k$ items into $n$ categories, which we can do by placing $n-1$ dividers between the $k$ items. We can re-frame this problem as selecting the locations of $n-1$ dividers from $(n-1)+k$ slots (items + dividers), which means our solution is $$\binom{n-1+k}{n-1} = \binom{n-1+k}{k}.$$
Note: Bose-Einstein is a bit of a “big hammer” — it can solve some pretty complicated problems, but also some simpler ones. You should make sure you have exhausted your other tools, and that your problem matches the “unordered, with replacement” requirement before trying this out.
3. Definitions of Probability
- The sample space $S$ is the set of all possible outcomes of an experiment (i.e., each element of $S$ is a unique outcome).
- After an experiment is completed, exactly one of the outcomes will have occurred.
- An event $A$ is any subset of $S$ ($A \subset S$) - anything that we could say either “happened” or “didn’t happen” once the experiment takes place. We calculate the probabilities of events (e.g., the probability that an event $A$ happens).
- After an experiment is completed, every event will have
- “Happened” or “happened” if it contains the outcome which actually occurred.
- “Not happened” or “not occurred” if it does not contain the outcome which actually occured.
- After an experiment is completed, every event will have
3.1 Naive Definition of Probability
Click for example
When rolling a standard die, the sample space is typically denoted by $S = \{1, 2, 3, 4, 5, 6\}$, where each element of $S$ is a possible outcome.
Possible events could be rolling a $1$ (the event being $A = \{1\}$), rolling an odd number, $B = \{1, 3, 5\}$, or rolling a small number $C = \{1, 2, 3\}$.
For a fair die, you might intuitively know that the probability of $A$ is $1/6$, the probability of $B$ is $3/6=1/2$, and the probability of $C$ is $3/6=1/2$. Also see that it’s possible that the events $A, B, C$ all occur, even though only one outcome actually occur.
We assume that there are a finite number of outcomes (the sample space, $S$, is finite), and that each individual outcome has an equal probability of occuring. Then the probability of an event $A$ is. $$ P_{\text{naive}}(A) = \frac{\text{# of outcomes in $A$}}{\text{# of outcomes in $S$}} = \frac{|A|}{|S|}. $$
Limitations:
- Assumes that all outcomes are equally likely
- Shaky definition of what “equally likely” means because we can arbitrarily construct the outcomes.
- ex. Say the weather tomorrow has two possible outcomes: $\{\text{precipitation}, \text{no precipitation}\}$. By the naive definition, there’s a $50%$ chance of no precipitation.
Alternatively, I could have said the possible outcomes are $\{\text{rain}, \text{sleet}, \text{hail}, \text{snow}, \text{no precipitation}\}$. Then there’s only a $20%$ chance of no precipitation… so which is it?
- Assumes the sample space is finite
- What if the sample space is of possible temperatures? There are infinitely many possible temperatures, they can’t each have a $1/\infty$ probability.
3.2 General Definition of Probability
Definition of probability:
There are just two axioms (rules that probabilities have to follow):
- $P(S) = 1, P(\emptyset) = 0.$
- If events $A_1, A_2, \ldots$ are disjoint, then $$ P\left( \bigcup_{j=1}^\infty A_j\right) = \sum_{j=1}^\infty P(A_j). $$
In other words, if $A_1, A_2, \ldots$ partition some event $B$, then $P(B) = \sum_{j=1}^\infty P(A_j)$.
3.2.1 Probability of Complements
Let’s say we know the probability of some event $A$. Then $$P(A^c) = 1 - P(A).$$ This follows directly from the axioms of probability: since $A^c, A$ partition the sample space $S$, we know $P(A) + P(A^c) = P(S) = 1$. When you’re asked to calculate the probability of events in the form of “at least” or “at most”, the probability of the complement may sometimes be simpler to calculate.
3.2.2 Principle of Inclusion-Exclusion (PIE)/Probability of unions
Say we have two events (not necessarily disjoint) $A$ and $B$. We can partition $A \cup B$ into $A \setminus B, A \cap B, B \setminus A$. \begin{align*} P(A \cup B) &= P(A \setminus B) + P(A \cap B) + P(B \setminus A)\\ P(A \cup B) &= P(A \setminus B) + P(A \cap B) + P(B \setminus A) + P (A \cap B) - P(A \cap B)\\ P(A \cup B) &= P(A) + P(B) - P(A \cap B), \end{align*} where we apply the second axiom of probability using the fact that $A \setminus B, A \cap B$ partition $A$ and the fact that $B \setminus A, A \cap B$ partition $B$.
This extends to finding the probability of the union of any $n$ events, which is called the Principle of Inclusion-Exclusion (PIE) \begin{align*} P(A_1 \cup A_2 \cup \cdots \cup A_n) &= \sum_{i=1}^n P(A_i) - \sum_{i<j} P(A_i \cap A_j) + \sum_{i < j < k} P(A_i \cap A_j \cap A_k) \\ &- \cdots + (-1)^{n-1} P(A_1 \cap A_2 \cap \cdots \cap A_n). \end{align*}
We are a bit careless with notation in the sums: $\sum_{i<j}$ means that we sum over every (unordered) pair of events. This formula is better remembered in words: add up the probabilities of all individual events, subtract the probabilities of every pair, add back the probabilities of every triple, etc.; remember that you start positive, then alternate signs.
PIE is another tool that is a big hammer: it will always work if you’re finding the probability of a union (the probability that at least one event occurs), but it is unwieldy for most problems and should be one of your last resorts.
4. Summary
4.1 Set Theory
- Sets: unordered collections of items
- Important set operations: intersection, union, complement, difference, cardinality
- Important properties: set membership, subsets, disjoint sets, partitions
- Theorems: DeMorgan’s laws
4.2 Counting
All of our counting is driven by the multiplication rule. Here’s what we’ve built from that, working from a set of $n$ distinct items:
| select how many items? | ordered or unordered? | with or without replacement? | solution |
|---|---|---|---|
| take all $n$ items, | order the items, | without replacement | n! |
| select $k$ items, | ordered, | without replacement | $\frac{n!}{(n-k)!}$ |
| select $k$ items, | unordered, | without replacment | $\binom{n}{k}$ |
| select any number of items, | unordered, | without replacement | $2^n$ |
| select $k$ items, | unordered, | with replacement | $\binom{n+k-1}{k}$ |
| select $k$ items, | ordered, | with replacement | $n^k$ |
You may also have seen this sampling table (below) in lecture (for counting the numbers of ways to draw a sample of $k$ items from $n$ distinct items). I suggest breaking down every counting problem into whether order matters and whether you are sampling with replacement, and trying out the corresponding approach in the table.
| Order matters | Order doesn’t matter | |
|---|---|---|
| With replacement | $n^k$ | $\binom{n+k-1}{k}$ |
| Without replacement | $\frac{n!}{(n-k)!}$ | $\binom{n}{k}$ |
We also talked about the permutation problem with $n$ items that aren’t necessarily distinct (order all $n$ items without replacement), where we compensate for overcounting after the fact: $$\frac{n!}{n_1! n_2! \cdots n_m!}.$$
4.3 Definitions of Probability
Naive probability: probably the most intuitive (and yet very flawed) way to define probability: the probability is proportional to the number of outcomes. For example, there are 3 ways to roll an even number on a die, so by this definition, there is a $3/6 = 1/2$ probability of rolling an even number.
(Non-naive) probability: given by two axioms:
- $P(S) = 1$
- $P\left(\bigcup_{j=1}^\infty A_j \right) = \sum_{j=1}^\infty P(A_j)$ for $A_1, A_2, \ldots$ disjoint.
The principle of inclusion-exclusion and the probability of complements follow from the axioms.
5. Practice Problems
Practice Problem Solutions PDF
I am interested in five subjects (statistics, math, computer science, chemistry, and biology) and am deciding between 100, 102, 110, and 111 in each department (e.g., my options are Stat 100, Stat 102, Stat 110, Stat 111, Math 100, Math 102, etc.). Assume unless stated otherwise that each class (or set of classes) is equally likely to be chosen if possible.
- How many different schedules of four courses can I take?
- I want to send my friend a text of my 4-class schedule. My text will look be a list like “Chemistry 101, Stat 110, Biology 111, Math 101”, which is considered a different text from “Stat 110, Chemistry 101, Biology 111, Math 101”. How many different such texts could I send?
- If I take 5 courses, what is the probability that I take exactly 1 course from each department?
- My advisor wants to know that I have backup plans, so they ask me to send 2 schedules with 4 courses each, where the schedules can have no overlap. How many such sets of two schedules can I send my advisor?
- After I finalize my schedule, my advisor now wants to know how many classes I’m taking in each subject, so I send them a list that follows the following format of the following example (with the subjects always in this order):
[Statistics: 2, Math: 0, Computer Science: 1, Chemistry: 1, Biology: 1]
How many such lists can I send for a 4-class schedule? - If I take 6 courses, what is the probability that there’s at least 1 subject in which I am not taking any courses? Solve this problem in two ways.
(Problem statement taken from Rachel Li and Ginnie Ma’s notes) Hockey Stick Identity: show using a story proof that $$ \sum_{j=k}^n \binom{j}{k} = \binom{n+1}{k+1}. $$ Hint: Imagine arranging a group of people by age, and then think about the oldest person in a chosen subgroup.
Use problem 1.4 to construct a story proof for the following identity (assuming $n \ge 2k$). Recall that in problem 1.4, my advisor asked me to make 2 (non-overlapping) schedules with 4 courses each. $$ \binom{n}{2k} \binom{2k}{k} = \binom{n}{k}\binom{n-k}{k} $$
5.1 Extra practice problems (if you have time during section)
Taken from the section materials of Rachel Li and Ginnie Ma (‘23)
(Lattice Walks) You start at the origin of a grid. Assuming you can only move up or to the right one unit at a time, how many different paths exist between you and position $(10, 10)$? Next, assume you are in a 3D-space. How many different paths exist between you and position $(10, 10, 10)$? Last, say your motions are defined by a 2-dimensional random walk: where you either walk right or up one unit with equal probability. After 20 steps, what is the probability that you are at position $(10, 10)$?
(Coin Toss Gambling, Question Credit: Zhou, 2008) Two gamblers are playing a coin toss game. Gambler A has $(n + 1)$ fair coins. Gambler B has $n$ fair coins. What is the probability that A will have more heads than B if they all flip their coins?
Hint: What are the possible results (events) if we compare the number of heads in A’s first $n$ coins with B’s $n$ coins? By making the number of coins equal, we can take advantage of symmetry. For each event, what will happen if A’s last coin is a head? Or Tails?(Teenager Steps) A teenage boy recently went through his first growth spurt, and can now walk up stairs one or two stairs at a time. How many different ways are there for him to ascend to the top of a staircase with $n$ stairs?
Hint: start with small $n$. The solution should look familiar!